
Gdyby małe dzieci znały się odrobinę na informatyce, rodzice na pewno straszyliby je nie kominiarzem, ale funkcją Ackermanna. Jest to wspaniały przykład ukazujący, jak pozornie „niegroźna” z wyglądu funkcja rekurencyjna może być „groźna” w użyciu.
Funkcję Ackermanna zazwyczaj definiuje się następującym wzorem rekurencyjnym:
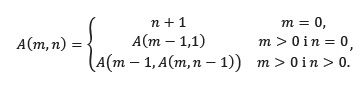
Przetestuj przykładowy program Ackermann.py pozwalający na wprowadzanie danych i odczytywanie wyniku (program zawiera podstawową kontrolę błędów). Sprawdź np., co się stanie, gdy podasz znak zamiast liczby:

Z pewnością zauważysz, że dla niektórych kombinacji parametrów wejściowych Python zgłosi błąd wykonania (np. „RecursionError: maximum recursion depth exceeded in comparison”). Ten ostatni komunikat jednoznacznie sugeruje, że podczas wykonywania programu nastąpiła znaczna liczba wywołań funkcji Ackermanna. Jak znaczna, okaże się już za chwilę.
Funkcja Ackermanna, nawet dla prostych wywołań, powoduje ból głowy!
Popatrzmy na pozornie proste wyliczenie wartości A(1, n):
A(1, n) = A(0, A(1, n − 1)) = A(1, n − 1) + 1 = A(0, A(1, n − 2)) +
+ 1 = A(1, n − 2) + 2 = … = A(0, A(1, 0)) + n − 1 = A(1, 0) + n = n + 2.
Podobnie karkołomne są wyliczenia wartości A(2, n):
A(2, n) = A(1, A(2, n − 1)) = A(2, n − 1) + 2 = A(1, A(2, n − 2)) + 2 = A(2, n − 2) +
+ 4 = … = A(1, A(2, 0)) + 2(n − 1) = A(2, 0) + 2n = 2n + 3.
Można udowodnić, że A(3, y) = 2n+3−3.
Wartość A(4, n) jest już makabrycznie wielka i wynosi 2⋰ − 3, gdzie liczba dwójek w wykładniku potęgi wynosi n+3.
Wyrażenie w formie liczbowej wartości A(4, 4) jest — co może będzie zbyt dyplomatycznym sformułowaniem — niezbyt oczywiste, nieprawdaż? W przypadku funkcji Ackermanna trudno nawet nazwać jej klasę. Stwierdzenie, że zachowuje się ona wykładniczo, może zabrzmieć jak kpina!
Dla osób zainteresowanych funkcją Ackermanna i jej własnościami podaję w tabeli schemat wzrastania wartości tej funkcji w zależności od parametrów m i n.

Po więcej zajrzyj do książki... ⬇️


